Kad čujemo reč trigonometrija, verovatno pomislimo na trouglove, dugačke izraze i nešto komplikovano i neupotrebljivo.
A da li je to zaista tako, ili se trigonometrija možda može posmatrati i na drugačiji način?
Naravno da može! To ćemo videti na ovoj prezentaciji.
Trigonometrija je jedna od najprimenjenijih grana matematike, a koristi se u arhitekturi, fizici, inženjerstvu, tehnici i svim granama nauke koje koriste geometrijska izračunavanja.
Reč trigonometrija potiče od grčkih reči trigonon, sto znači trougao, i metron, sto znači mera.
Kao što joj samo ime kaže ona se bavi merenjem trouglova, a ovde ćemo je posmatrati i preko krugova i uglova da bismo je bolje razumeli.
Prvi put u istoriji je zabeležena između 1900. i 1600. godine pre nove ere, kada su njenu "proto" verziju koristili stari Egipćani da bi gradili piramide.
Da, trigonometrija je upotrebljivana čak tada, i pomoću nje sagrađene su poznate piramide koje pridadaju najvećim građevinama svih vremena.
Egipćani nisu imali sastavljenu celu trigonometriju kakvu danas poznajemo, ali koristili su njene delove kako bi opisali odnose u trouglovima kako bi gradili piramide.

Dakle, već u tom periodu istorije, trigonometrija se koristila, mada Egipćani nisu računali vrednosti funkcija uglova. Oni su je koristili da bi opisali odnose u trouglu.
Prvi koji su upotrebili trigonometriju za izračunavanje bili su Grci. Oni su prvi upotrebili funkcije koje danas znamo.
Grčki matematičar Hipokrit posmatrao je tetive kruga i centalne uglove.
Hteo je da nađe dužinu tetive, ili osnovicu jednakokrakog trougla ako mu je poznat krak i ugao pri vrhu.
Pogledajmo sliku:
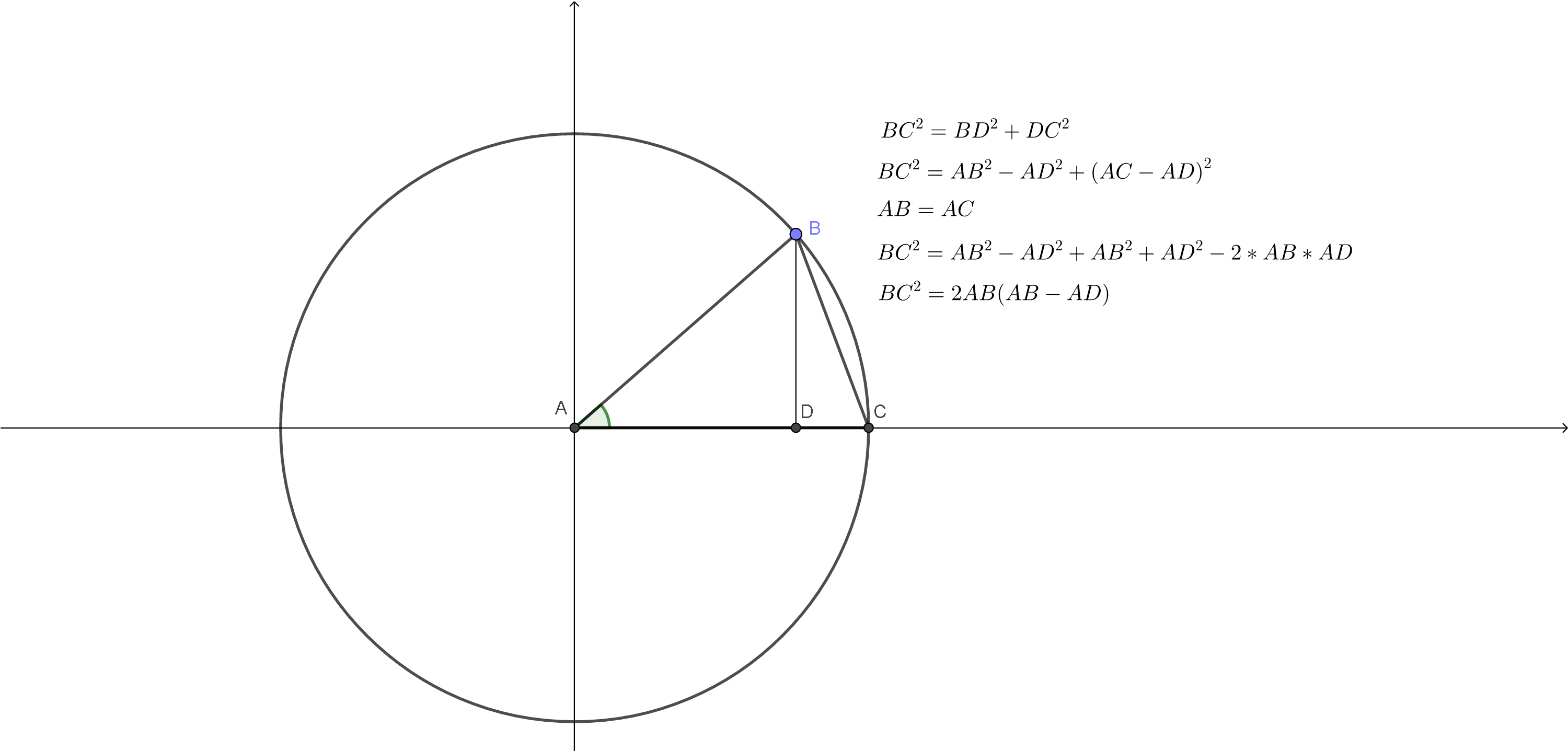
Pomoću Pitagorine teoreme, može se naći tetiva BC kruga sa centrom u A poluprečnika AB.
To se može uraditi samo sa poznatim poluprečnikom AB i duži AD.
Kako bismo našli ovu dužinu ne moramo koristiti trigonometriju, ovde je upotrebljena samo Pitagorina teorema.
Ali, na ovom primeru Grci su prvi put upotrebili oznake kosinus i sinus.
Pogledajmo kako su to uradili na sledećoj stranici.